由于每次看QQ图,都简单的介绍这样的图是好,这样的图是不好,不够学术,所以基于我现在的知识,简单介绍一下我对QQ图和曼哈顿图的理解。
#理解QQ图模型是否合理:
QQ plot的全称是Quantile-Quantile Plot,即分位数图。在GWAS分析里面,QQ plot的纵坐标是SNP位点的pvalue值,即观测到的pvalue,与曼哈顿图一样也是表示为-log10(pvalue);横坐标则是均匀分布的概率值,即期望的pvalue,同样也是换算为-log10。
QQ图比较的是Pvalue观测值(Y轴)和Pvalue期望值的一致性。直观解读就是:判断图形中点的分布是否合理(是否位于对角线上),进而推断目前的统计模型获得的P 值是否符合期望值以及统计模型是否合理。
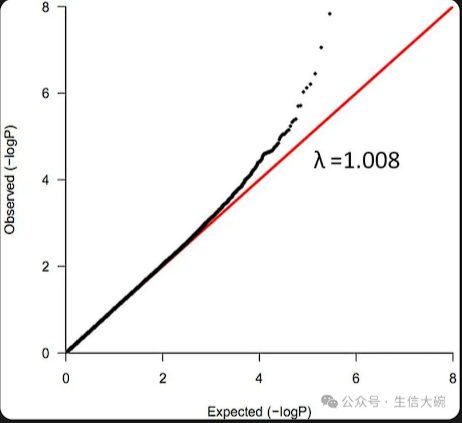
如上图所示是最理想的结果,在散点图的左下角是显著性低的位点,即确定与性状不关联的位点,这些位点的pvalue观测值应该与期望值一致,正好图中这些点位于对角线上,说明分析模型是合理的。在散点图的右上角则是显著性较高的位点,是与性状相关的潜在候选位点,这些点位于对角线的上方,即位点的pvalue观测值超过了期望值,说明这些位点的效应超过了随机效应,进而说明这些位点是与性状显著相关的。
再列举几个QQ图示例:
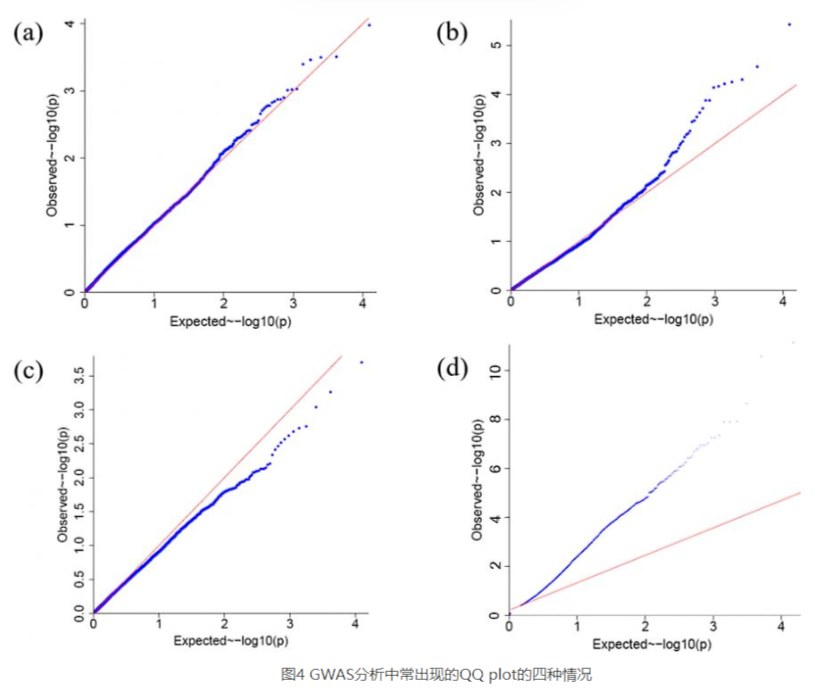
(a)pvalue观察值和期望值相同,说明分析模型是合理的。但所有的pvalue观测值都没有明显超过期望值,说明分析结果没有找到(与性状)显著关联的位点,可能原因包括:性状由微效多基因控制,效应太弱;群体大小不够等。
(b)是我们最期望看到的结果类型。在散点图的左下角是显著性低的位点,即确定与性状不关联的位点,这些位点的pvalue观测值应该与期望值一致。而图中这些点的确位于对角线上,说明分析模型是合理的。而在图形的右上角则是显著性较高的位点,是潜在与性状相关的候选位点。这些点位于对角线的上方,即位点的P value观测值超过了期望值,说明这些位点的效应超过了随机效应,进而说明这些位点是与性状显著相关的。
小结一下:这个图形的左下角说明了模型的合理性,右上角则说明找了关联位点,所以这是最理想的结果。
(c)是大部分点位于对角线的下方,则说明大部分位点的pvalue观察值小于期望值。主要原因包括两种情况:(1)模型不合理,pvalue被过度校正,导致pvalue显著性过低;(2)群体中大量SNP位点间存在连锁不平衡,有效位点数(相互间不存在连锁不平衡的位点)明显低于实际位点数,所以pvalue的期望值被低估了(即期望值的-log10(pvalue)被高估了),也会出现这种情况。
(d)与c图则相反:大部分点位于对角线的上方,则说明大部分位点的pvalue观察值超过期望值。按照统计学的逻辑推导,就是大部分位点与某个性状显著相关。这显然是不符合生物学逻辑的,那么这只有一种可能:分析模型不合理,数据的假阳性过大,pvalue观测值的显著性被高估了。
凡是出现图4(c)和图4(d)的情况,则需要检查分析模型是否有问题,群体中是否有某些干扰因素没被考虑到分析模型中(例如,群体结构、系谱关系、性别等),在重建分析模型后重新分析。
#理解QQ图模型背后的概念:
QQ图是用来协作判断GWAS结果的好坏的,准确的说 是用来描述是否与表型性状相关。
QQ图的均匀分布恰好可以用来描述基因组上的随机漂变现象。如果表型性状并非真的受自然选择所左右,那么你应该会看到GWAS pvalue的分布和均匀分布的结果将集中在一条直线上,如果不是那么就应该能够看到相互分离的情况,特别是palue越低的时候分离程度就越高,QQ-plot会翘起来(这是因为GWAS的零假设就是与随机突变相比没有区别)。
而且,我们知道基因组上的随机漂变是一定存在的,所以一定会有位点与随机漂变相关,特别是是在pvalue比较大的位点看起来就应该和随机漂变重叠,这就表现在QQ-plot的前半部分里。这位点的分布会和均匀分布重叠。而且,比较好的结果是,当pvalue < 10^-3时,GWAS结果开始与均匀分布出现快速分离——也就是说,自然选择的力量明显地显示出来了,使得结果在群体中快速摆脱随机性,最后看到一个高高翘起的QQ-plot。这时基本就可以断定,我们所研究的表型和基因型之间是存在着显著相关的自然选择作用的。
#曼哈顿图:
在GWAS的研究中,Pvalue的阈值一般设置在10-6或者10-8以下,也就说曼哈顿图中Y轴大于6甚至大于8的那些SNP位点才是比较值得研究的,具体也要看你的实际数据表现。
参考: